Hermanos Juramentados de la Espada Negra
- Inicio
- Novelas
- Juego de rol
- Juego de mesa
- Música
- Galeria
- Enciclopedia
- FAQ
- Contacto
- Hermandad
- Uso y licencias

Probabilidades de éxito en uniones e intersecciones
29-9-2015 13:18
Por Verion
Hoy voy a escribir un pequeño artículo de matemáticas muy básicas. Llevo bastante sin hacerlo, y no he visto este asunto escrito en ningún lado. Es algo que nos afecta en los juegos de rol como jugadores, y creo que puede ser una información interesante.
A lo largo de este texto voy a facilitar la forma de hacer los cálculos que nos permitirán responder a dos preguntas interesantes, y también facilitaré los métodos para calcular los casos generales, aunque supongo que la mayoría de los excelentes lectores ya los conocerían de sobra dada su experiencia con los juegos.
Dado una prueba en la que participan N personas idénticas, en la que todos fracasan si uno fracasa, ¿cual es la probabilidad de éxito?
Bueno, esto suena un poco extraño, pero pongamos un ejemplo. Imaginemos que queremos infiltrarnos en el campamento de nuestros enemigos y matar al general. Si los centinelas ven a un solo hombre infiltrarse, darán la alerta y todo el plan fracasará.

La trampa de todo esto es que vamos a suponer la independencia de los sucesos a la hora de hacer los cálculos, y esto no es así. Cuando un grupo toma una acción así los resultados interfieren, en algunos casos para bien (técnicas conjuntas) y en otros para mal (uso de espacios limitado). Pero en los juegos de rol los chequeos no suelen ser tan sofisticados, así que para el caso nos puede servir.
La matemática en este caso es muy sencilla. Si cada hombre tiene una probabilidad de éxito P, expresada en probabilidad “por uno” (esto es, un 80% equivale a 0.80), la probabilidad final es el producto de dichas probabilidades. Dicho de una forma final:
Probabilidad final = P^N
Podemos elaborar una tabla y ver que efectivamente cuantos más hombres llevemos más difícil es que nuestra misión tenga éxito.
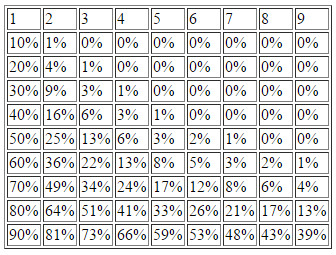
(Aclaración sobre cómo interpretar esta tabla: Si una persona tiene un 80% de éxito -bajo la columna 1- entonces tres personas con esa probabilidad tienen en conjunto un 34% todas juntas)
Esto no es solo aplicable a la cuestión citada, sino que puede entenderse en un marco más general para tácticas que requieren varios pasos que han de tener éxito. Por ejemplo, supongamos que tenemos una táctica en un partido de blood bowl que exige que nuestro personaje tenga éxito en seis tiradas de 1D6 con cuatro resultados válidos en cada una de ellas (66%). El resultado final, pues, es de un mísero 8%. Ni se moleste en intentarlo.
Por cierto, que es muy fácil extrapolarlo a cálculos en los que las probabilidades de cada elemento son distintas: solo hay que multiplicarlas todas.
Ah, y seguramente a los más estrategas les interesen los valores más allá del noventa por ciento. Aquí están:
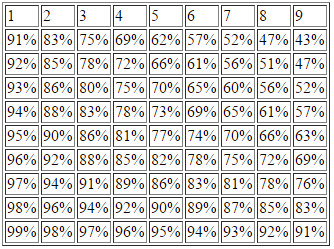
Dado una prueba en la que participan N personas idénticas, en la que todos tienen éxito si uno tiene éxito, ¿cual es la probabilidad de éxito?
Vamos a ver qué significa esto con un ejemplo. Se trata de una situación en la que hay una puerta con una cerradura, y los personajes intentan forzar la cerradura uno a uno, y de forma independiente. Si uno lo consigue, la puerta se abre y todos pasan.

En realidad calcular esta probabilidad es bastante complejo, pero sin embargo calcular la probabilidad contraria, la de que todos fracasen e simple. Dado que P sea la probabilidad de cada uno de ellos de tener éxito (como antes), la de que cada uno de ellos fracase es la complementaria 1-P, y por lo tanto la de que fracasen todos es:
Probabilidad de que fracasen todos = (1-P)^N
Y como nos interesa la complementaria:
Probabilidad final = 1-(1-P)^N
Elaboremos, pues, una tabla con estos resultados y veamos la probabilidad definitiva.
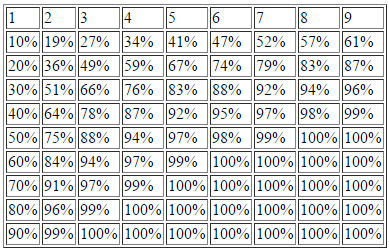
A mí estos resultados me parecen interesantes porque son muy sencillos, son extrapolables a cualquier juego e incluso a la vida real. Nos dicen que para cosas muy básicas en las que vale con que un elemento tenga éxito es mejor tener muchos elementos poco preparados que un elemento fuertemente preparado (que cada cual encuentre su ejemplo), sin embargo para asuntos delicados (como una complicada operación de neurocirugía o hacer funcionar el LHC) es necesario que todos los elementos tengan una probabilidad de éxito muy muy cercana al ciento por ciento.
Y aunque quizá sea útil para que los jugadores planteen sus posibles estrategias, también puede ser una interesante herramienta para planear juegos que se acerquen un poco más a la causalidad natural de los sucesos.
Entradas similares:
A lo largo de este texto voy a facilitar la forma de hacer los cálculos que nos permitirán responder a dos preguntas interesantes, y también facilitaré los métodos para calcular los casos generales, aunque supongo que la mayoría de los excelentes lectores ya los conocerían de sobra dada su experiencia con los juegos.
Dado una prueba en la que participan N personas idénticas, en la que todos fracasan si uno fracasa, ¿cual es la probabilidad de éxito?
Bueno, esto suena un poco extraño, pero pongamos un ejemplo. Imaginemos que queremos infiltrarnos en el campamento de nuestros enemigos y matar al general. Si los centinelas ven a un solo hombre infiltrarse, darán la alerta y todo el plan fracasará.
La trampa de todo esto es que vamos a suponer la independencia de los sucesos a la hora de hacer los cálculos, y esto no es así. Cuando un grupo toma una acción así los resultados interfieren, en algunos casos para bien (técnicas conjuntas) y en otros para mal (uso de espacios limitado). Pero en los juegos de rol los chequeos no suelen ser tan sofisticados, así que para el caso nos puede servir.
La matemática en este caso es muy sencilla. Si cada hombre tiene una probabilidad de éxito P, expresada en probabilidad “por uno” (esto es, un 80% equivale a 0.80), la probabilidad final es el producto de dichas probabilidades. Dicho de una forma final:
Probabilidad final = P^N
Podemos elaborar una tabla y ver que efectivamente cuantos más hombres llevemos más difícil es que nuestra misión tenga éxito.

(Aclaración sobre cómo interpretar esta tabla: Si una persona tiene un 80% de éxito -bajo la columna 1- entonces tres personas con esa probabilidad tienen en conjunto un 34% todas juntas)
Esto no es solo aplicable a la cuestión citada, sino que puede entenderse en un marco más general para tácticas que requieren varios pasos que han de tener éxito. Por ejemplo, supongamos que tenemos una táctica en un partido de blood bowl que exige que nuestro personaje tenga éxito en seis tiradas de 1D6 con cuatro resultados válidos en cada una de ellas (66%). El resultado final, pues, es de un mísero 8%. Ni se moleste en intentarlo.
Por cierto, que es muy fácil extrapolarlo a cálculos en los que las probabilidades de cada elemento son distintas: solo hay que multiplicarlas todas.
Ah, y seguramente a los más estrategas les interesen los valores más allá del noventa por ciento. Aquí están:

Dado una prueba en la que participan N personas idénticas, en la que todos tienen éxito si uno tiene éxito, ¿cual es la probabilidad de éxito?
Vamos a ver qué significa esto con un ejemplo. Se trata de una situación en la que hay una puerta con una cerradura, y los personajes intentan forzar la cerradura uno a uno, y de forma independiente. Si uno lo consigue, la puerta se abre y todos pasan.
En realidad calcular esta probabilidad es bastante complejo, pero sin embargo calcular la probabilidad contraria, la de que todos fracasen e simple. Dado que P sea la probabilidad de cada uno de ellos de tener éxito (como antes), la de que cada uno de ellos fracase es la complementaria 1-P, y por lo tanto la de que fracasen todos es:
Probabilidad de que fracasen todos = (1-P)^N
Y como nos interesa la complementaria:
Probabilidad final = 1-(1-P)^N
Elaboremos, pues, una tabla con estos resultados y veamos la probabilidad definitiva.

A mí estos resultados me parecen interesantes porque son muy sencillos, son extrapolables a cualquier juego e incluso a la vida real. Nos dicen que para cosas muy básicas en las que vale con que un elemento tenga éxito es mejor tener muchos elementos poco preparados que un elemento fuertemente preparado (que cada cual encuentre su ejemplo), sin embargo para asuntos delicados (como una complicada operación de neurocirugía o hacer funcionar el LHC) es necesario que todos los elementos tengan una probabilidad de éxito muy muy cercana al ciento por ciento.
Y aunque quizá sea útil para que los jugadores planteen sus posibles estrategias, también puede ser una interesante herramienta para planear juegos que se acerquen un poco más a la causalidad natural de los sucesos.
Entradas similares: